PROYECTO – CARTEL – OIM

Teorema aplicado al diseño.

Mi enfoque sobre este proyecto es el siguiente: Realizar un cartel la OIM (Olimpiada Internacional de Matemática), anunciando y promocionando el evento para este año 2012 – 2013, utilizando el teorema de Bolzano.

Apartado de diseño:

Apartado matemático:

Teorema de Bolzano o teorema de los valores intermedios.

En análisis matemático el teorema del valor intermedio (o más correctamente teorema de los valores intermedios, o TVI), es un teorema sobre funciones continuas reales definidas sobre un intervalo. El resultado afirma que, si una función es continua en un intervalo, entonces toma todos los intermedios comprendidos entre los extremos del intervalo.

Enunciado:

Sea f una función continua en un intervalo [a,b]. Entonces para cada u tal que f (a) < u < f (b), existe al menos un c dentro de (a,b) tal que f (c) = u.

Enunciados equivalentes:

Si f es una función continua a valores reales definida sobre el intervalo [a,b], y u es un número entre f (a) y f (b), entonces existe un c perteneciente a [a,b] tal que f (c) = u.

Si f es una función continua en el [a,b], y f (a) tiene signo opuesto a f (b), existe un punto c, tal que su imagen es 0.

Como consecuencia del teorema de Weierstrass, se puede generalizar diciendo que la imagen de un intervalo es otro intervalo.

Historia:

El teorema fue demostrado por primera vez por Bernard Bolzano en 1817. Cauchy da una demostración en 1821.Ambos perseguían el fin de formalizar el análisis de funciones y el trabajo de Lagrange. La idea de que las funciones continuas poseen la propiedad del valor intermedio es de larga data. Simon Stevin probó el teorema del valor intermedio para polinomios por medio de un algoritmo para construir la expansión decimal de la solución: el algoritmo subdivide el intervalo iterativamente en 10 partes, lo que produce un dígito decimal adicional en cada paso de la iteración. Antes de que la definición formal de continuidad existiera, la propiedad del valor intermedio era dada como parte de la definición de función continua. Otros autores asumían que el resultado es intuitivamente obvio, por lo que no requiere de prueba. La visión de Bolzano y Cauchy fue la de definir una noción general de continuidad (en términos de infinitesimales en el caso de Cauchy, utilizando desigualdades reales en el caso de Bolzano), y la de proveer una prueba basada en tales definiciones.

El recíproco del teorema es falso. No es necesario que una función sea continua para que la conclusión del teorema de los valores intermedios sea cierta. En 1875, Darboux demuestra que las funciones que provienen de una derivada, sean continuas o no, poseen la propiedad de los valores intermedios.

PROYECTO – CARTEL – 4D TYPE

Sistemas representativos

Mi enfoque sobre este proyecto es el siguiente: Realizar un cartel para presentar la tipografía 4D Type del estudio de diseño gráfico LoSiento Studio.

Apartado de diseño:

La tipografía 4D es el resultado de intersecar, de manera ortogonal en el espacio, dos protuberancias del mismo carácter, lo que permite al espectador leer desde dos posiciones diferentes en el espacio.

Para disfrutar de una arquitectura espacial, el observador se ve obligado a moverse a través de ella. El cambio en la administración perspectiva genera nuevos espacios en los que la luz actúa de diferentes maneras. En este caso, es la tipografía la que hace el esfuerzo de abandonar sus dos dimensiones para abordar el sentido arquitectónico. Son necesarias cuatro dimensiones para completar las posibilidades de lectura. Al colgar la tipografía, se permite al lector rodear los caracteres con el fin de comprender todas sus formas.

Este hombre es el autor de esta genial tipografía, se llama Gerard Miró, diseñado y matemático. Y la página web de su estudio es la siguiente: http://www.losiento.net/entry/4d-type

Apartado matemático:

‘Dibujar el espacio en el plano’.

Los sistemas perspectivos o perspectivas, basándose en las claves espaciales (altura, anchura y profundidad), utilizan métodos matemáticos que sirven para representar o imitar la realidad tridimensional en un papel bidimensional (altura y anchura).

Cuando dibujamos la realidad, utilizamos ‘trucos’ para que los objetos tengan la apariencia de profundidad.

Para este diseño he utilizado fundamentalmente la perspectiva axonométrica ortogonal trimétrica. La excepción es la última perspectiva (Abajo a la derecha en la composición), representación de la figura en planta (Sistema diédrico).

El concepto de proyección, determina el proceso por el que se obtiene una imagen sobre un plano, de una figura bidimensional o tridimensional situada en el espacio.  En las proyecciones cilíndricas los rayos proyectantes son paralelos entre sí. El sistema axonométrico está conformado por dos grandes bloques de perspectivas axonométricas: La primera de ellas, la axonometría ortogonal, se denomina así por estar basada en una proyección cilíndrica ortogonal; la segunda, la axonometría oblicua, se fundamenta en una proyección cilíndrica oblicua. Para este diseño he utilizado únicamente el primer tipo, perspectiva axonométrica ortogonal que puede ser isométrica, dimétrica y trimétrico, en función del ángulo que separe los ejes, en este caso son todas trimétricas. Ya que son tres ángulos diferentes los que separan los ejes dos a dos.

Proyecto - Portada Libro - Collar Tangencial

COLLAR DE ÁRBELOS O CADENA DE PAPPUS.

El apartado matemático gira entorno a la construcción de un collar basado en tangencias, el apartado de diseño, es una ilustración para la portada de un libro de Adrián Paenza titulado ‘Matemática… ¿Estás ahí’.

APARTADO MATEMÁTICO.

El triángulo curvilíneo que aparece en la siguiente imagen, formado por tres semicircunferencias mutuamente tangentes, con sus centros alineados sobre la misma recta era conocida entre los antiguos griegos como 'Árbelos', que significa 'Cuchilla de zapatero', por su similitud con la que utilizan esos profesionales para cortar cuero. Según parece, fue Arquímedes el que primero la estuda, y posteriormente, también es tratada por Pappus, Vieta, Descartes, Fermat, Newton , Steiner y McKay, y ya en el siglo XX, por Victor Thébault, Leon Bankoff, ClaytonW. Dodge, Thomas Schoch, Peter Y. Woo y Paul Yiu.

Considerando un segmento AB, y C un punto cualquiera de su interior trazamos los semicírculos de diámetros AB, AC y CB se obtenemos el árbelos.

Me propongo enumerar algunas de las numerosas propiedades del árbelos, relacionadas con los contenidos vistos en clases: Tangencias, arco capaz, el teorema de la altura, inversión, rectas tangentes exteriores a dos circunferencias.

Levantemos por C una perpendicular a AB hasta que corte a la circunferencia mayor en T. Unamos C con A y con B. Sean X e Y las intersecciones con las dos circunferencias pequeñas. Unamos X con Y, y sea O la intersección de las diagonales del cuadrilátero  CT y  XY.

1) EL ARCO CAPAZ - El cuadrilátero XCYT es un rectángulo.

Como los  ángulos AXC (α) = ATB (β) = CYB (γ) = 90º, por tratarse de ángulos inscritos que abarcan una semicircunferencia (Propiedad del arco capaz), XCYT es un rectángulo.

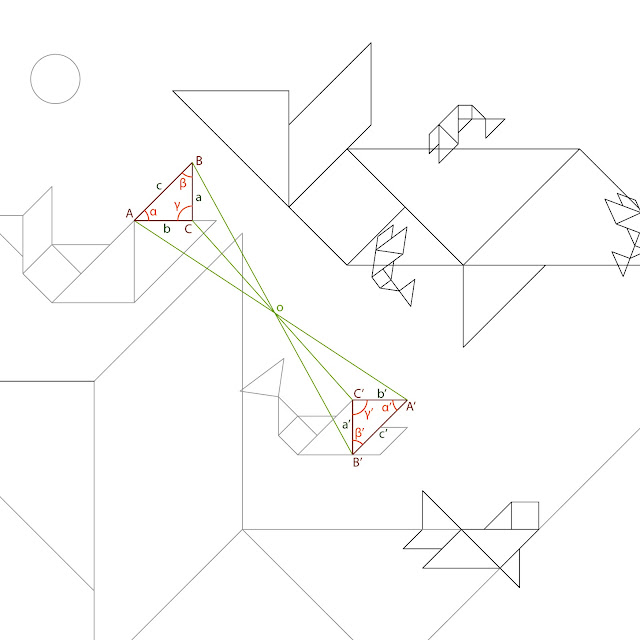
2) ÁNGULOS Y TRIÁNGULOS - La recta XY es tangente a los círculos de diámetros AC y BC.

Para demostrar que XY es tangente a los dos círculos, es suficiente probar que XY es perpendicular a XD e YE. Siendo D y E los centros de los círculos de diámetros AC y CB. El radio es perpendicular a la tangente en el punto de tangencia.

El triángulo formado por los vértices XDC, es isósceles, porque DX = DC, ambos son radios; y OXC es isósceles también, porque OX y OC son semidiagonales de un rectángulo. Siendo O el punto de intersección y el punto medio de las rectas diagonales XY y CT. Entonces tenemos que α = β, pasa lo mismo con los siguientes ángulos γ = δ. En definitiva, el ángulo DXY = α + γ = β + δ = DCT = 90º, pues la recta CT es perpendicular a AB. Análogamente se probaría que es tangente al de diámetro CB.

3) EL TEOREMA DE LA ALTURA - El área del árbelos es igual a la del círculo de diámetro CT.

Llamaremos r a la recta AO’ (Siendo O’ el punto medio del segmento AB), r1= AD y r2 = CE. Tenemos que AD + CE = AO’ ó r1 + r2 = r.

Por otro lado el área del árbelos= π/2 (r² - r1² - r2²) = π/2 ((r1-r2)² - r1² - r2²) = πr1r2.

Y ahora sí, el teorema de la altura (Es decir, la semejanza entre los triángulos rectángulos ACT (Azul) y BCT (Rojo) permite escribir: (CT/AC) = (CB/CT); CT² = AC x CB. Por tanto el área del círculo de diámetro CT vale: π (CT/2)² = (π/4) x CT² = (π/4) x AC x CB = (π/4) x 2r1 x 2r2 = πr1r2, idéntico al área del árbelos.

4) CIRCUNFERENCIA INTERIOR TANGENTE A OTRAS TRES CIRCUNFERENCIAS.

Si M y N son los puntos medios de los arcos AC y CB, con centro en M y radio MA se traza una circunferencia que pasa por A,C,Q y R; con centro en N y radio NB se traza otra circunferencia que pasa por B,C,P y R. Los tres puntos de tangencia buscados son P,Q y R. El círculo inscrito en el árbelos es el circunscrito a PQR.

5) CURIOSIDAD. Los círculos mellizos de Arquímedes: el inicio de una familia numerosa.

Arquímedes descubrió dos círculos inscritos en el árbelos que tienen el mismo radio (Trazo naranja).

En 1974, Leon Bankoff  encontró un trillizo (Trazo verde) y pronto el cuatrillizo (Trazo amarillo).

A partir del cuatrillizo, han seguido apareciendo nuevos círculos notables, hasta formar una familia infinita. Otro ejemplo es el mellizo (En rojo) del circulo de diámetro CT (Apartado 3), en el cual están inscritos los mellizos de Arquímedes.

6) CONSTRUCCIÓN DEL COLLAR O CADENA PAPPUS.

Partiendo de la figura del árbelos, lo primero que necesitamos es construir la circunferencia de inversión, para ello se traza desde C una recta (r, en rojo) perpendicular a AB, hasta que interseque  con el arco mayor, obteniendo el punto K. La circunferencia con radio AK (k, en azul), es la que utilizaremos para reflejar (o invertir), los puntos.

Trasladamos los puntos C, B y H, respecto al vector v (En naranja). Luego los reflejamos respecto a k para obtener C’k, H’k y B’k,  tres puntos (De tangencia), por los que pasa la segunda circunferencia, el segundo eslabón.

Para el segundo, trasladamos C’, B’ y H’, de nuevo respecto al vector v, obteniendo C’’, B’’ y H’’, estos los reflejamos y obtenemos los puntos C’’k, B’’k y H’’k, por los que pasa la tercera circunferencia.

7) RECTAS TANGENTES EXTERIORES A DOS CIRCUNFERENCIAS.

Para lograr las rectas tangentes exteriores (s y r) a dos circunferencias (Una amarilla, con centro en 01 y otra verde oscuro, con centro en 02), comenzamos restando r1 (El radio pequeño) a r2 (El radio mayor) y así tenemos r3.

Trazamos una circunferencia de r3 concentro en 02 (Color verde claro). Y calculamos las rectas tangentes a esta nueva circunferencia con respecto a O1 (Centro de la circunferencia amarilla). Para ello localizamos la mitad del segmento 0102, el punto M, y desde M trazamos una circunferencia (Gris) de radio M01 o M02, ambos son radios y logramos donde corta a la circunferencia verde claro, los puntos de tangencia A y B.

Unimos A y B con O2, a continuación prolongamos las rectas hasta que corten a la circunferencia verde oscuro, obteniendo los puntos de tangencia C y D. Para hallar los puntos de tangencia en la circunferencia amarilla trazamos por C una paralela a O1A y tenemos E. De igual modo por D una paralela a O1B, y ahora también tenemos F. Para dibujar s unimos EC y para r FD.

Proyecto - Ilustración - Formas Planas

Este proyecto parte de la siguiente premisa: Realizar un trabajo de diseño gráfico sobre las formas planas, jugando con la composición de las mismas. Justificar el fundamento científico de las relaciones y propiedades de las mismas.

Mi enfoque sobre este proyecto es el siguiente: Realizar una ilustración que integre únicamente formas planas, pero, que entremezcle formas geométricas y formas orgánicas.

1.  Apartado Diseño.

Bienvenido a mi Mundo Geométrico.

El diseño de esta ilustración tiene como objetivo crear una imagen que acompañará a un texto, ambos se publicarán digitalmente, en un blog. En cuanto lo tenga, añadiré aquí el link.

2. Apartado matemático.

- Intro: En esta imagen incluyo los diferentes tipos de triángulos y cuadriláteros, situados, a modo de muestrario.

Análisis de las formas que aparecen:

Por otro lado incluyo 2 relaciones diferentes entre una circunferencia y un triángulo: El arco capaz y la circunferencia de nueve puntos, también llamado círculo de Euler.

El arco capaz es el lugar geométrico de los puntos (Vértices) que unidos con los extremos de un segmento forman siempre un mismo ángulo. Como conclusión podemos deducir que todos los ángulos inscritos en una circunferencia que abarquen un mismo arco son todos iguales (α=β=δ=σ).

En geometría se conoce como circunferencia de nueve puntos a la circunferencia que se puede construir sobre cualquier triángulo (Salvo que el triángulo sea obtusángulo) cuando pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo: El punto medio de cada lado del triángulo (3 ptos), el pie de cada altura (3 ptos); y el punto medio de cada segmento que une el ortocentro (Intersección de las alturas) con los vértices del triángulo (3 ptos). Detalle, el centro de esta circunferencia se sitúa sobre la recta de Euler.

La recta de Euler de un triángulo es aquella que contiene al ortocentro, al circuncentro y al baricentro del mismo. Se llama así en honor al matemático suizo Leonhard Euler, quien descubrió este hecho a mediados del siglo XVIII.

Proyecto - Portada CD - Relaciones Geométricas Básicas Y Diseño

Este proyecto parte de la siguiente premisa: Realizar un estudio de diseño sobre las transformaciones geométricas básicas. Un estudio de los grupos de transformaciones (Proporción, escala, semejanza, homotecia, giros, traslaciones y simetrías). Un ejemplo de un trabajo puede ser el teorema Bravais, que abarca los conceptos de simetría, identidad y giro. O bien, un diseño sobre la proporción aurea y su aplicación a la estética. Los fundamentos científicos del número de oro.

Mi enfoque sobre este proyecto es el siguiente: Partir de la portada de un cd de música (Gojira, ‘Form Mars To Sirius’), y elaborar una portada alternativa basada en animales marinos formados por geometrías básicas (Tangram), realizando un análisis matemático de las relaciones entre las formas.

1.  Apartado Diseño.

Portada original del grupo (Joe Duplantier).

Diseño personal de portada.

2. Apartado matemático.

- Intro: Los triángulos de color verde (1er apartado) explican la relación de homotecia, proporción y escala. Los triángulos de color rojo (2º apartado) explican la simetría central y la razón de semejanza. Las figuras en naranja (3er apartado) explican el teorema de Bravais (Simetría axial, identidad y giro).

- Homotecia, proporción,  escala y Thales.

El triángulo 1 y el 2 están relacionados mediante el centro de homotecia O1, lo cual quiere decir que sus segmentos relativos son paralelos y proporcionales (a/a’=b/b’=k) y que las dimensiones del triángulo 2 están escaladas con respecto a las del triángulo 1 (En este caso k=1/4=0.5). (Más adelante aparecerá una homotecia de razón negativa, cuando lleguemos a la simetría central).

La relación de proporcionalidad entre ambos triángulos puede definirse de la siguiente manera: O1A/O1A’=O1B/ O1B’=k, o también: O1A’/A’B’=O1A/ AB=k.

Los triángulos 1 y 3 están en posición de Thales.  Por este motivo son proporcionales y homotéticos entre sí. La peculiaridad es que ambos tienen un ángulo, un vértice en común, y este también coincide con el centro de homotecia  (B≡B’’≡O2).

Al trabajar con triángulos, también podemos hablar del criterio de semejanza. En esta imagen los triángulos 1, 2 y 3 son semejantes entre sí. Los criterios de semejanza aparecen a continuación detallados, al hablar de la simetría central.

- Simetría central y criterio de semejanza.

Ambos triángulos están vinculados por una simetría central de centro en el punto O.  A y A’ son puntos homólogos ya que O es el punto medio del segmento que los une a ambos. De igual modo B y B’ o C y C’ también son puntos homólogos ya que OA=OA’, OB=OB’ y OC=OC’.

En una simetría central, los segmentos homólogos son iguales (a=a’, b=b’ y c=c’) y la medida de los ángulos correspondientes también son iguales (α=α’, β=β’ y γ=γ’).

Son triángulos homotéticos (Con centro de homotecia en O). La razón homotética que relaciona el segundo triángulo con respecto al primero es -1/1.

Ambos triángulos también son semejantes. Se llama criterio de semejanza de dos triángulos a las de condiciones tales que si se cumplen, tendremos la seguridad de que los triángulos son semejantes:

- Primer criterio: Dos triángulos son semejantes si tienen dos pares de ángulos respectivamente iguales (α=α’, β=β’ y γ=γ’).

- Segundo criterio: Dos triángulos son semejantes si sus lados son proporcionales (a/a’=b/b’=c/c’).

-Tercer criterio: Dos triángulos son semejantes si tienen un ángulo igual y los lados que lo forman son proporcionales (α= α’ y a/a’=b/b’).

- Teorema De Bravais (Simetría axial, identidad y giro).

Las tres figuras forman grupo.  La figura 2 es simétrica a la figura 1 mediante el eje 1 de simetría axial. La fig. 3 es simétrica a la  fig. 2 mediante el eje 2 de simetría. El teorema de Bravais demuestra como mediante un giro podemos obtener a partir de la fig. 1, la. fig 3, siendo el centro de giro (O) la intersección de los ejes de simetría 1 y 2.

En una simetría axial para hallar el punto simétrico (A’) de un punto (A), se traza una recta (r) perpendicular al eje de simetría (Eje1) que pase por el punto (A). La intersección entre esta recta (r) y el eje (Eje1), produce un punto (P). Partiendo de este punto (P) sobre la recta (r) llevamos la distancia que hay entre el punto del que partíamos (A) y el punto intersección (P). De tal forma que AP = PA’ y A’Q=QA’’.

Un Movimiento es una transformación (Una correspondencia de puntos, A-A’’ y B-B’’) en la que la forma y tamaño de las figuras resultan invariables. Las simetrías (A-A’ y B-B’ o A’-A’’ y B’-B’’) se consideran movimientos inversos porque no conservan la orientación de la figuras. El movimiento de la fig. 3 con respecto a la fig. 1, es un movimiento negativo (Giro en el sentido de las agujas del reloj) y directo (Este desplazamiento conserva el sentido de los ángulos).